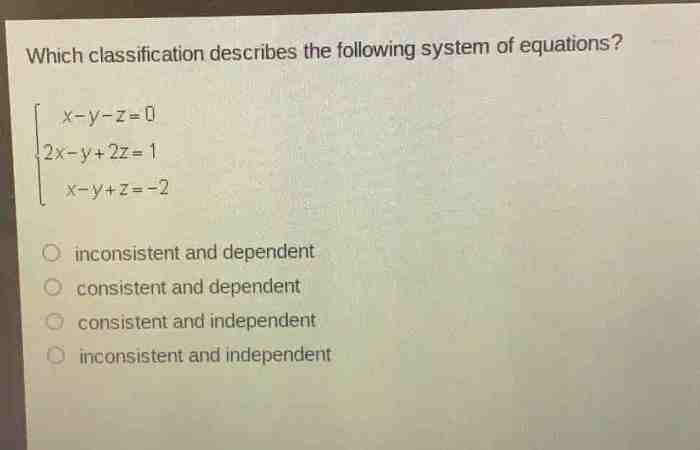
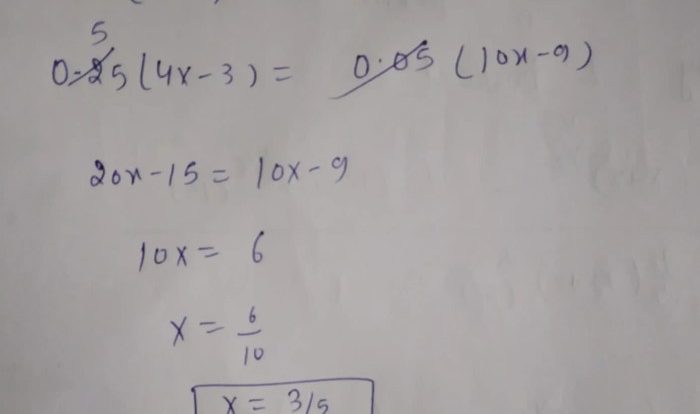Which classification describes the following system of equations – Delving into the realm of equation classification, we embark on a journey to decipher the nature of various systems of equations. This exploration will unravel the intricacies of linear, quadratic, polynomial, exponential, and logarithmic equations, unveiling their defining characteristics and the criteria that govern their classification.
Systems of equations, composed of multiple equations with shared variables, present a unique challenge. We will delve into the methods employed to solve these systems, including substitution, elimination, and matrices, showcasing their application through illustrative examples.
Equation Classification Identification
Equation classifications provide a framework for understanding the properties and behavior of mathematical equations. These classifications are based on the structure and complexity of the equations, and they guide the choice of appropriate solution methods.
Linear Equations
- First-degree equations
- Variables appear only in the first power
- Example: 2x + 5 = 11
Quadratic Equations
- Second-degree equations
- Variables can appear in the second power, but not higher
- Example: x^2 – 5x + 6 = 0
Polynomial Equations, Which classification describes the following system of equations
- Equations with variables raised to integer powers
- Degree is determined by the highest exponent
- Example: x^3 – 2x^2 + 5x – 1 = 0
Exponential Equations
- Equations involving exponential functions (e^x)
- Variables appear as exponents
- Example: 2^x = 16
Logarithmic Equations
- Equations involving logarithmic functions (log(x))
- Variables appear as arguments of logarithms
- Example: log(x) + log(x+2) = 1
System of Equations: Which Classification Describes The Following System Of Equations

A system of equations consists of two or more equations that involve the same variables. Solving a system of equations means finding values for the variables that satisfy all the equations simultaneously.
Methods for Solving Systems of Equations
- Substitution
- Elimination
- Matrices
Example:
Solve the system of equations:
x + y = 5
2x – y = 1
Using the elimination method:
- Multiply the first equation by 2 to get 2x + 2y = 10.
- Add the second equation to the new first equation to get 4x = 11.
- Solve for x: x = 11/4.
- Substitute x back into the first equation to get y = 5
- x = 5
- 11/4 = 9/4.
Therefore, the solution to the system of equations is (x, y) = (11/4, 9/4).
System Classification

Systems of equations can be classified based on the number of solutions they have:
Consistent Systems
- Have at least one solution
- Can be either independent or dependent
Inconsistent Systems
- Have no solutions
- Equations represent parallel lines or planes
Independent Systems
- Have exactly one solution
- Equations represent intersecting lines or planes
Dependent Systems
- Have infinitely many solutions
- Equations represent coincident lines or planes
Example:
Classify the following system of equations:
x + y = 2
2x + 2y = 4
This system is dependent because the second equation is a multiple of the first equation. Therefore, it has infinitely many solutions.
Table Presentation
| Classification | Key Characteristics | Examples |
|---|---|---|
| Linear | First-degree equations | 2x + 5 = 11 |
| Quadratic | Variables in the second power | x^2
|
| Polynomial | Variables raised to integer powers | x^3
|
| Exponential | Exponential functions (e^x) | 2^x = 16 |
| Logarithmic | Logarithmic functions (log(x)) | log(x) + log(x+2) = 1 |
Helpful Answers
What is the key characteristic of a linear equation?
A linear equation exhibits a constant slope and a constant y-intercept.
How can you determine if a system of equations is inconsistent?
An inconsistent system of equations has no solutions, resulting in parallel lines or intersecting lines at a single point.